B 스플라인 보간법(B-spline interpolation)은 입력된 데이터 포인트들을
이용하여 부드러운 곡선 혹은 표면을 만드는 수학적인 방법입니다.
B 스플라인은 선형보간(linear interpolation)보다 더 부드러운 곡선을 만들어내며,
다항식 보간법(polynomial interpolation)보다는 계산적으로 안정적입니다.
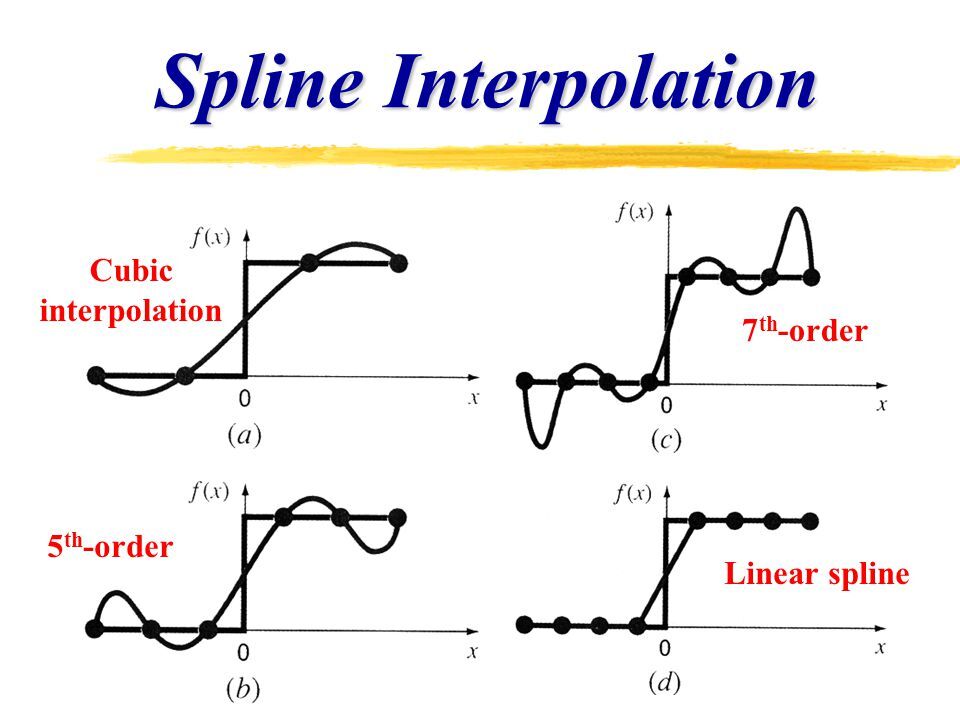
B 스플라인은 세부적인 조정을 통해 곡선의 부드러움 정도를 조절할 수 있으며,
데이터 포인트의 개수와 B 스플라인의 차수(degree)를 조절하여
보간법의 정확도와 부드러움 정도를 조절할 수 있습니다.
B 스플라인은 주로 컴퓨터 그래픽스, CAD, 컴퓨터 비전 및 이미지 처리 등의 분야에서 사용됩니다.
B 스플라인은 다음과 같은 단계로 수행됩니다.
1. 데이터 포인트를 입력합니다.
2. B 스플라인의 차수와 노드 벡터(node vector)를 정합니다.
3. B 스플라인 기저함수(B-spline basis function)를 계산합니다.
4. 입력된 데이터 포인트를 이용하여 B 스플라인 보간곡선(interpolating curve)을 계산합니다.
B 스플라인은 선형보간과 다항식 보간법의 단점을 보완하고
부드러운 곡선을 만들어내는 장점이 있습니다.
하지만, B 스플라인은 입력된 데이터 포인트 사이를 지나지 않으므로
보간된 곡선이 데이터 포인트 사이에서 완벽하게 일치하지는 않습니다.
간단한 예제 코드 첨부합니다.
import numpy as np
from scipy.interpolate import BSpline
# Define x and y data
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 3, 1, 2])
# Define degree of B-spline
k = 3
# Define knot vector
t = np.array([1, 1, 1, 2, 3, 4, 5, 5, 5])
# Create B-spline object
spline = BSpline(t, y, k)
# Define x values to interpolate at
x_interp = np.linspace(x.min(), x.max(), 100)
# Interpolate y values
y_interp = spline(x_interp)
# Plot original data and interpolated data
import matplotlib.pyplot as plt
plt.plot(x, y, 'o', label='Data')
plt.plot(x_interp, y_interp, label='B-spline')
plt.legend()
plt.show()